Church-Rosser and Combinatory Logic

Church-Rosser Theorem

If $M$ reduces to both $N$ and $P$, then there exists a $Q$ for which both terms reduce to (but not necessarily in one step). 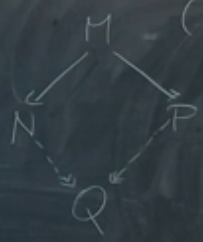Every binary relationship has the diamond property if this holds: 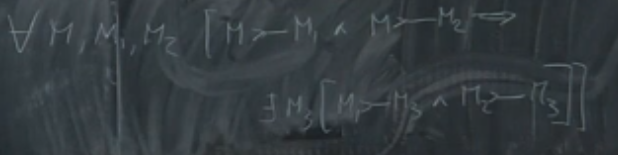$\beta$ reduction doesn’t have the diamond property. 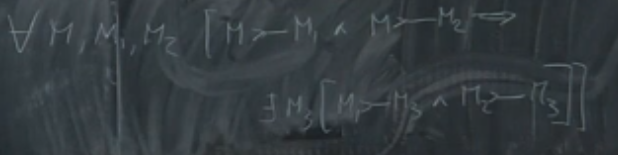Graphically, this is the diamond property, because the relationship above the diamond and below is not the same (one step beta reduction vs many step beta reduction).

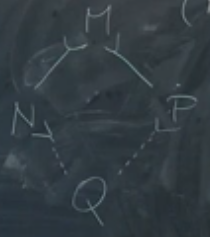
#todo continue

Combinatory Logic

#todo: describe combinatory logic

An abstraction algorithm is an ordered sequence of rules that allow us to convert a term from lambda calculus to combinatory logic. We start from the beginning and we see which is the first rule that we can apply, apply it, and then start again from the beginning. In general this ordered sequence of rule is called Markov Algorithm. The algorithm stops when no further rule can be applied.

We start from the inside most term, to the outside.

Example

Let’s convert the term $\lambda xy.y$.

The abstraction algorithm in this case is defined as:

$$\begin{array}{rlr}[x]x=I& & \\ [x]U=KU& & \text{if }x\notin U\\ [x]UV=S([x]U)([x]V)& & \end{array}$$

and the conversion as:

$$\begin{array}{rlr}[x]([y]y)& & \text{I just rewrite the term}\\ [x](I)& & \text{I apply the first rule}\\ KI& & \text{I apply the second rule}\end{array}$$

If there are multiple variables in the lambda term (for example $\lambda xyz.x(yz)$, we first abstract form $z$, then we abstract the result from $y$ and then the result from $x$.

The following is another example in order to convert the term $\lambda xyz.x(yz)$

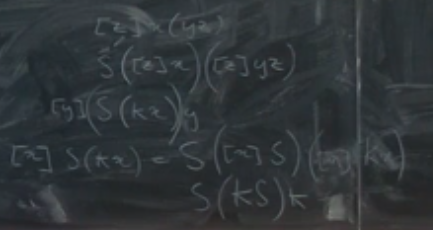
Once converted, we can verify that we are correct by giving 3 inputs to the combinatory term that we obtained, and see if the combination matches the one from the lambda term.

---

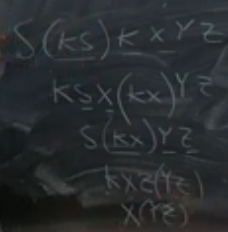
tags:#lambda-calculus