Markov Random Field
In a Undirected Graphical Model (undirected graph), meaning their connection between nodes are bidirectional, and can be interpreted as functions .
For example in this UGM:
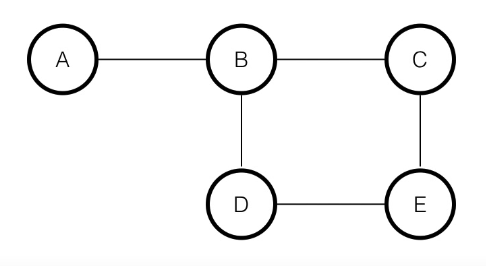 We can write the joint probability between all the variables in the graph can be factorized as following:
We can write the joint probability between all the variables in the graph can be factorized as following:
and so we can compute the marginal probability of a single variable as:
Where a clique is just a subset of the nodes in the graph where each couple of nodes is adjacent (the subgraph is complete).
Markov Random Fields are a class of Undirected Graphical Models, which obey the Markov property:
- Any two subsets and of the graph are conditionally independent given a separating subset (subset for which there doesn’t exist a path between and that doesn’t travel trough it) From this property other properties (corollaries) can be derived:
- Any two non-adjacent variables are conditionally independent given all other variables.
- Any variable is conditionally independent of the other variables given its neighbours (this is another form of the Markov blanket).
tags:#probability-theory -#graph-theory references: