Lamport Clock

The problem that the Lamport clock is trying to solve is how can $P_0$ take a snapshot of a consistent run in order to only detect real deadlocks.

Trying to find the solution

We assume that all the processes have access to a global clock (that’s something that doesn’t exists, but we make this assumptions to try to solve the problem)

First solution (complicated it’s not convenient): $P_0$ sends a message like “send me the local state in the $t_p$ timestamp. So the process $p$ waits until the timestap to send the local state.

Another solution is to set a time $t_0 + \Delta$ and capture the snapshot in that instant. The problem is what if the message doesn’t arrive in time? We has to try again, and that’a a problem. This would work in case of existance of a global clock, that makes sure that no future messages can be send to the past.

Global clock doesn’t exist, so we need another solution.
</details>

[!Clock Condition] If $e\to e’$ then $TS(e)<TS(e’)$ where $TS$ is the timestamp. Note that the arrow in the other way is not true, since if the two events are not correlated nor one or the other happens before the other, they’re concurrent.

The clock condition is always true if there is a global clock, but since processes in a distributed system don’t have access to a global clock, there is a need to invent a new type of clock that has the clock condition.

Every time an event occurs in a process, it labels it with a serial number (1,2,3 etc.). If a process $P_1$ makes an event that sends a message to a process $P_2$, $P_2$ labels it with the next number of the greatest next number between $P_1$ and $P_2$.

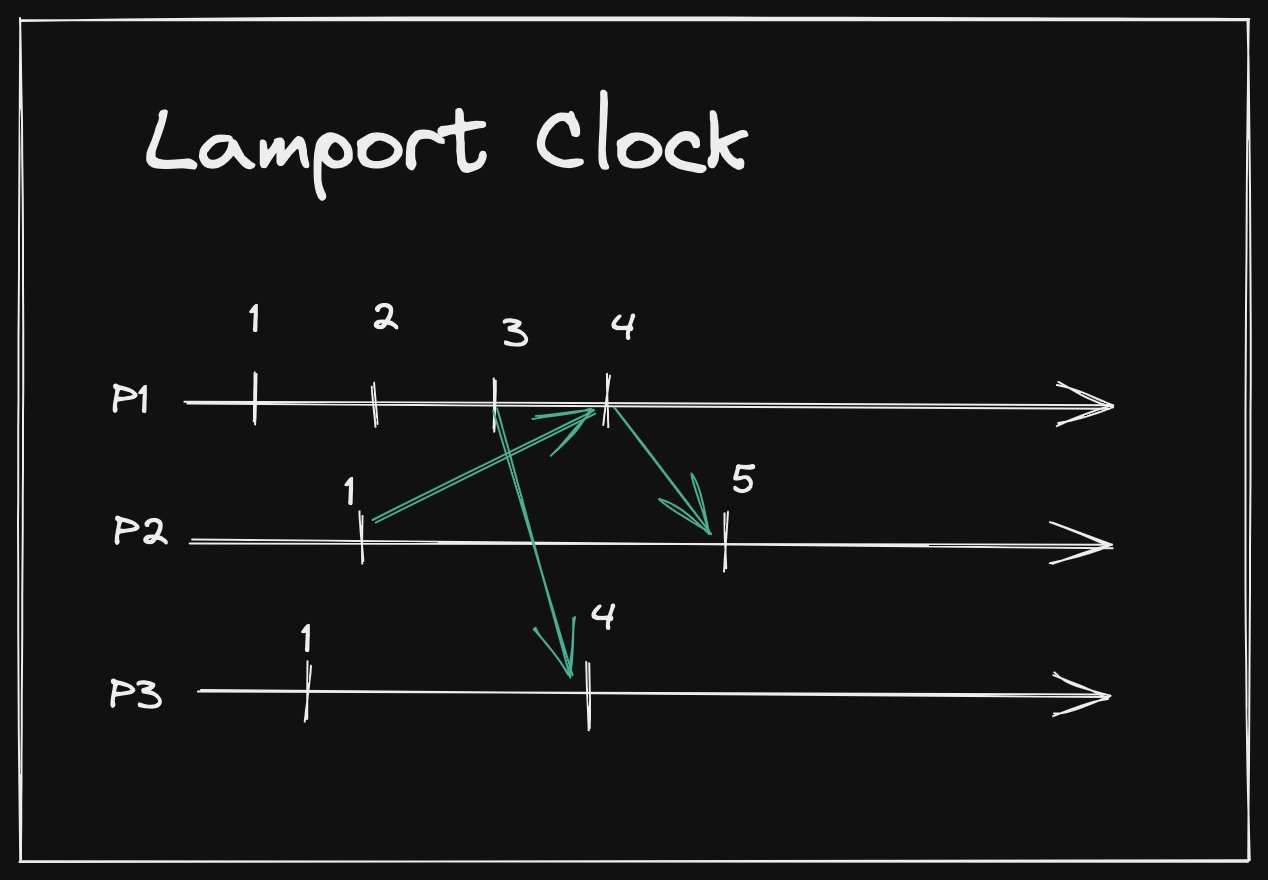
In this way, $P_0$ can reconstruct the run in a consistent one, and the problem is solved without the use of a global clock.

This new clock that we discovered is called Lamport clock, invented by Lamport in the 70s.

The order that $P_0$ sees may be slightly different from the real order, but it’s important since the order change happens between non-correlated events, so the two runs are both consistent.

Logical Clocks and stable messages

A Lamport clock is a type of logical clock. Logical clocks are all clocks that have the clock condition.

When $P_0$ receives a message, we make a difference between receiving and delivering:

• Received means that the messages arrive at $P_0$, but other messages previous to that one may still arrive in the future
• Delivered means that the message is accepted by $P_0$ and can be processed since no other messages previous to that one can arrive in the future;

$P_0$ will deliver a message $m$ only if it’s stable.

[!Stable Message] Message $m$ is stable at $p_i$ if no message $m^{\prime }$ such that $TS(m^{\prime })<TS(m)$ can arrive in the future.

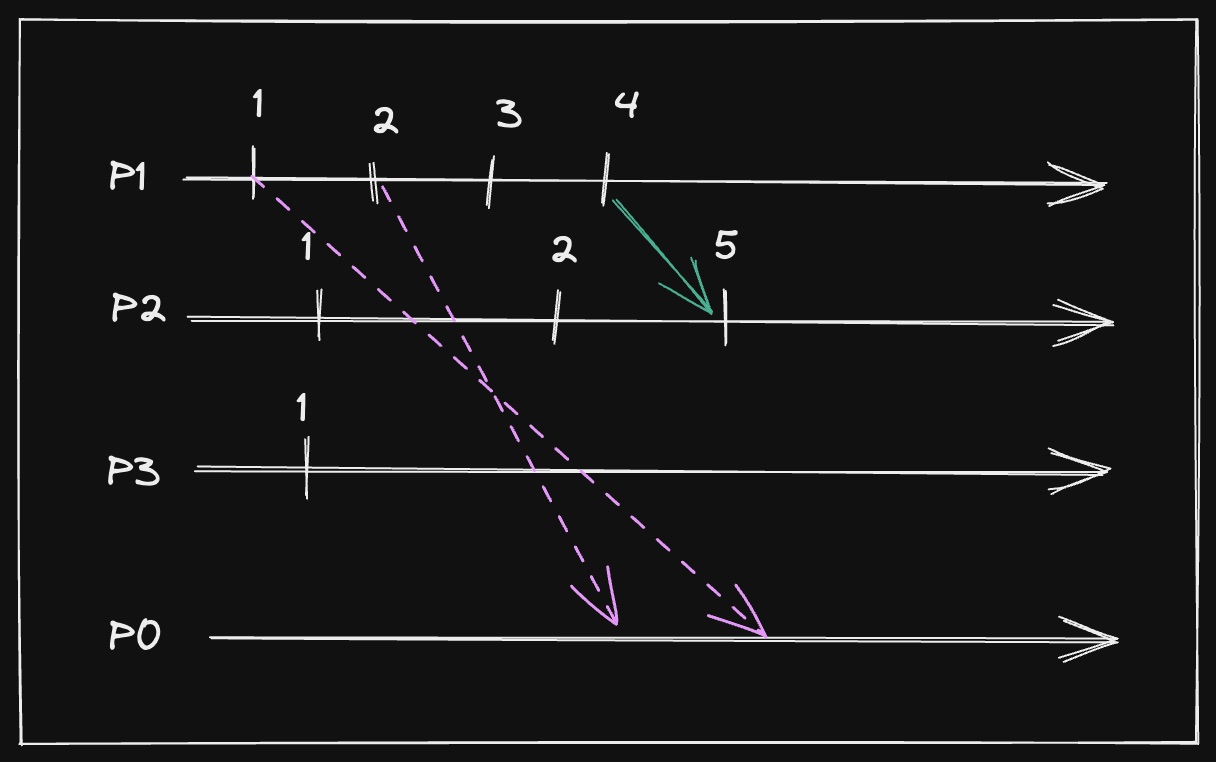
The received message 2 is not stable because I still can receive a 1 in the future, and 1 < 2.

A way that $P_0$ can recognize a message as stable is to implement channels as FIFO (First In First Out), in this way when it receives a message, it knows that all the previous messages have already arrived.

We define the array $D[i]=\text{highest TS received from process }i$ . In the start, $D$ is composed of zeros and has the length of the number of processes.

In this way, a message received from $P_0$ is stable only if all the other values in the vector are greater than the $TS$ of the message received. That’s because in order to deliver a message, all the messages with the $TS$ lower than the received message have to be delivered too, since the current message may depend on one of them.

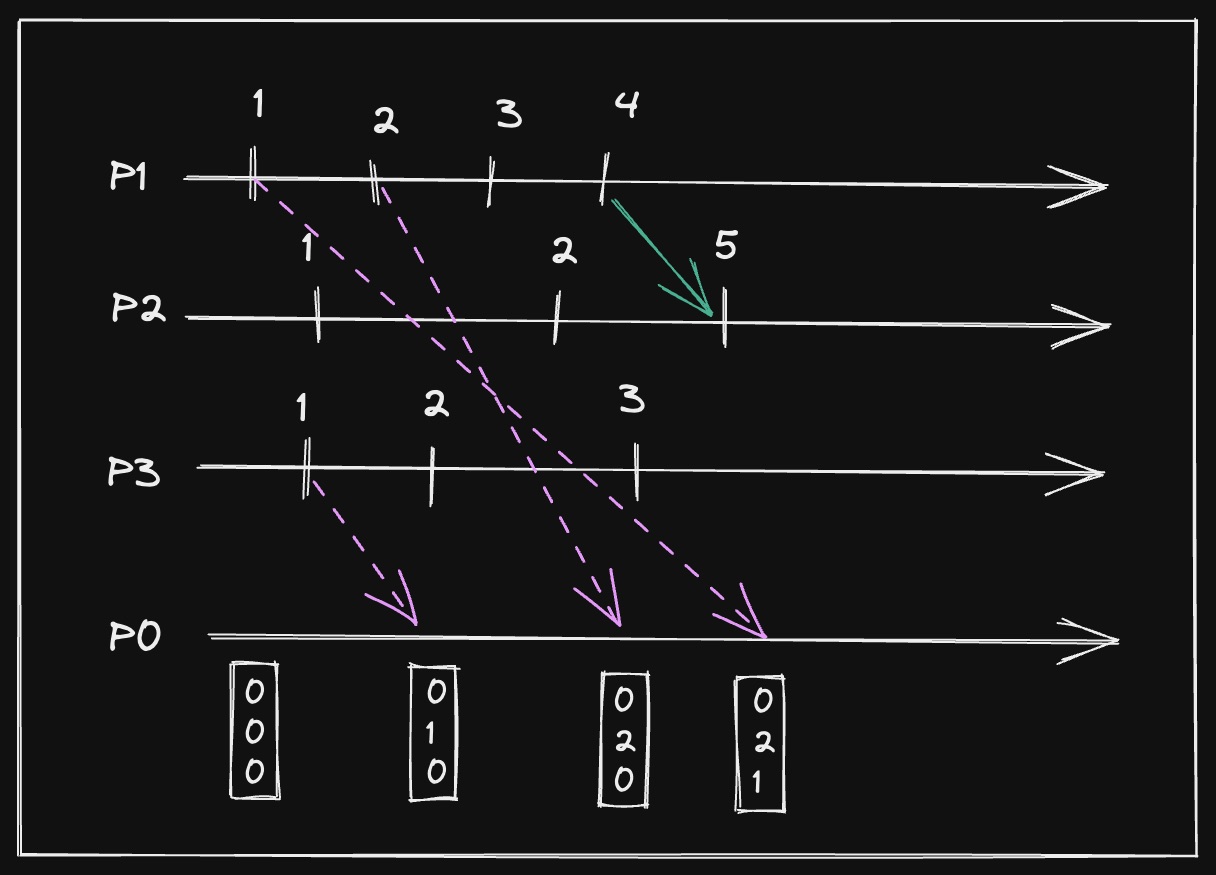
Todo

TODO: Change the vectors because they’re wrong

This is a solution but it’s not perfect, since it can raise some problems.

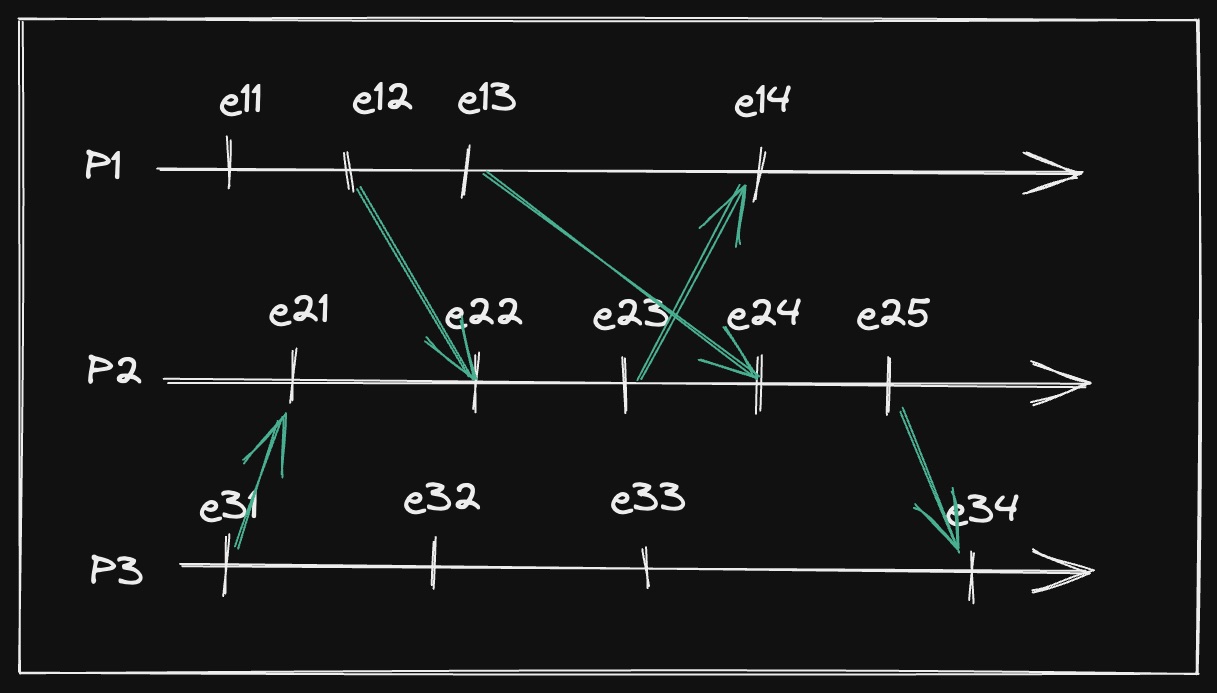
The first problem is that, in order to deliver a message, the process has to wait for all the processes with lower TS to arrive, and this could cause the process to wait forever to deliver a message.

This can happen because a message with a low $TS$ doesn’t arrive because of a failure.

Another cause could be seen in the picture: the message from $P_2$ with $TS=5$ will not be delivered until a message with $TS=4$ is received from $P_1$ and $P_3$, and since $P_3$’s last message has $TS=3$, it will wait forever.

Strong clock condition

A strong clock condition is a clock condition that is valid in both ways.

$$e\to e^{\prime }\iff TS(e)<TS(e’)$$

Logical clocks don’t have this condition:

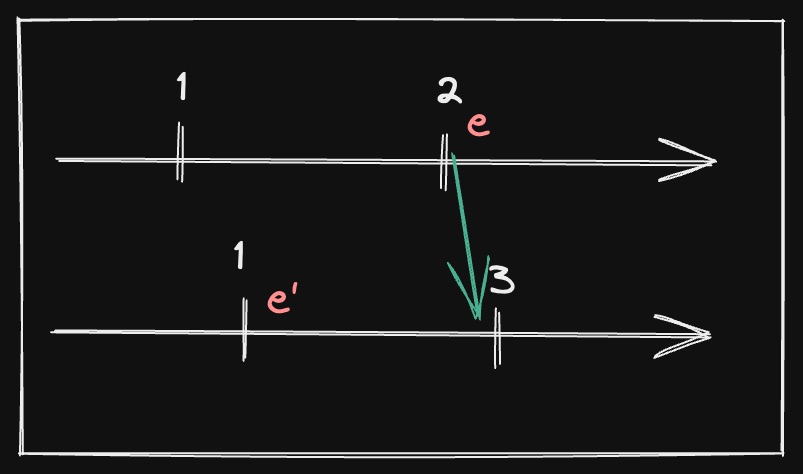
In this picture, we can see how $TS(e^{\prime })<TS(e)$ but it’s not true that $e^{\prime }\to e$, since they’re concurrent.

If two events in two processes are concurrent, it’s hard to assign them a numerical $TS$.

As we can see from the picture below, the timestamps 4-5 or 6-5 are not right because no event happens before one another. I cannot give them 5-5 because if then another event happens I would have 5-6, but it’s not true that the event with $TS=6$ on the first process happens before the event on process 2 with $TS=5$.

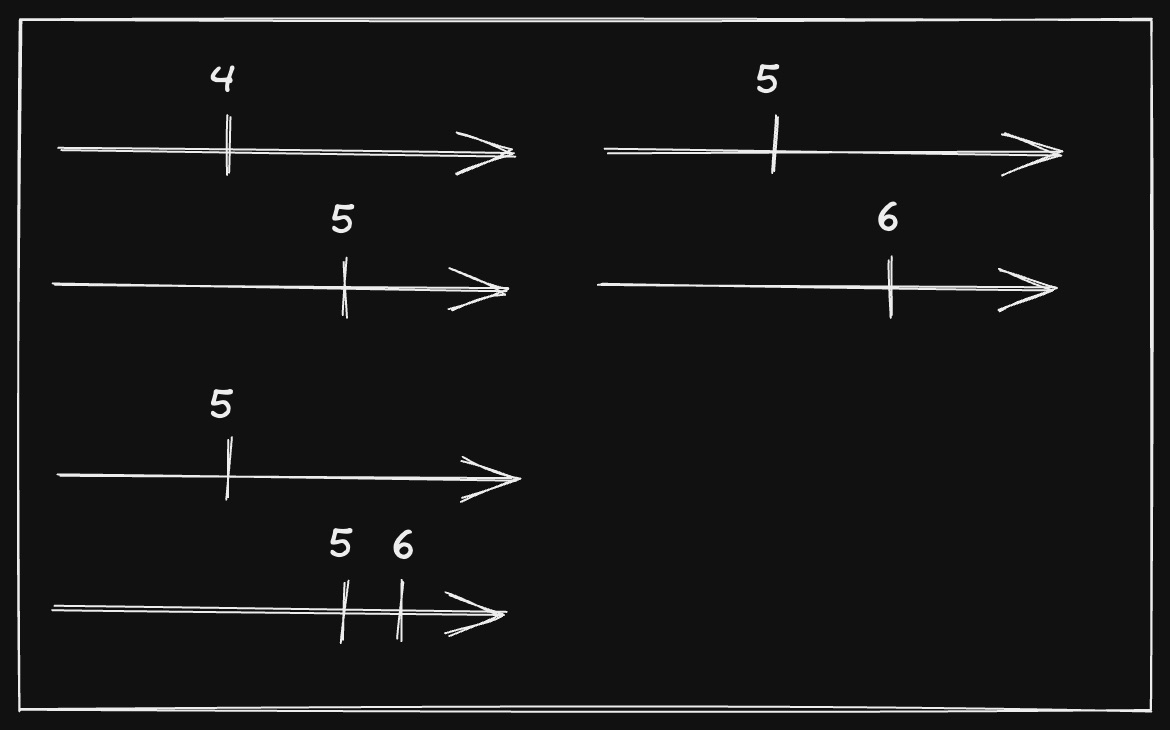
So we arrived at the fact that a numerical $TS$ is not enough in order to have a strong clock condition.

Causal history

Note

🔁 Causal history of an event $e$ $\theta (e)=\{e^{\prime }\in H:e^{\prime }\to e\}\cup \{e\}$

The causal history is the set of events that may have contributed to the event $e$.

$$\begin{gathered} \theta (e_1^1)=\{e_1^1\} \\ \theta (e_2^1)=\{e_3^1,e_2^1\} \\ \theta (e_2^2)=\{e_1^2,e_1^1,e_2^1,e_3^1,e_2^2\} \end{gathered}$$

Note

If $e\to e^{\prime }\Rightarrow \theta (e)\subseteq \theta (e^{\prime })$ It’s true also in the other direction, since $\theta (e)\subseteq \theta (e^{\prime })\Rightarrow e\in \theta (e^{\prime })\Rightarrow e\to e^{\prime }$ So it’s true that $e\to e^{\prime }\iff \theta (e)\subseteq \theta (e^{\prime })$

In order to avoid the problems that the solution above raised, we can timestamp the messages with their causal history.

This obviously can bring problems with efficiency, since the causal history of an event can be very big.

Vector clock

To solve the problem of the causal history is big, we can timestamp an event not with the entire history, but with just the last event that’s part of the history, In this way all the other past processes in history become implicit.

Note

🕰️ Vector clock: $VC[i]=\text{internal clock of the latest event inside process }i$

This type of clock has a strong clock condition.

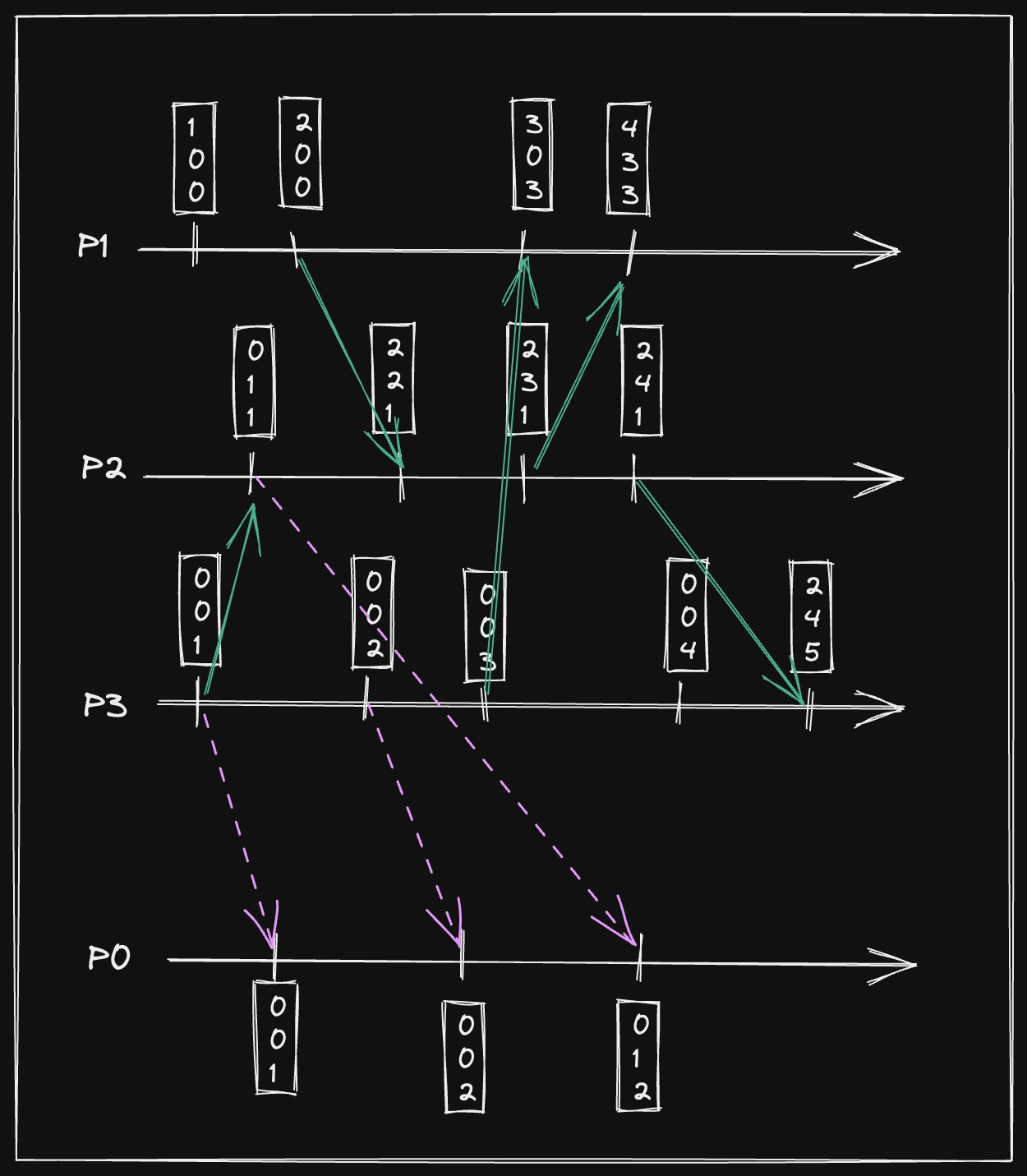
Computed vector clocks for all the events in the processes

If the vector is of the type $[0,0,2]$, $P_0$ know that this is the 2nd message sent by $P_3$, and it knows that that message doesn’t depend on $P_1$ or $P_2$, since the values on those positions are zeros.

In case the last $VC$ is $[0,1,2]$ and $P_0$ receives $[2,2,1]$ it cannot receive it because the message depends on two messages of $P_1$ that it didn’t receive yet.

With the Vector Clock, $P_0$ can deliver all the messages that can be delivered, different from before.

The vector that $P_0$ keeps to keep track means $[i,j,k]$ i received $i$ messages from $P_1$, $j$ messages from $P_2$, and $k$ messages from $P_3$. The vector that $P_0$ keeps is not a TS, but it’s only a vector to make a comparison with the VC it will receive.