PCA - Principal Component Analysis

PCA - Principal Component Analysis

The curse of dimensionality is solved in the feature space with dimensionality reduction methods, such as Principal Component Analysis (PCA).

What PCA does is to transform the data by creating a new space in which the axis are the $n$ principal components of the data, where $n$ is the number of dimensions.

These principal components are the eigenvectors with the highest eigenvalues, this models the direction where the data variance is higher. The first PC is the one with the highest eigenvalue, the second is the one just under that and so on. A PC is just a linear combination of all the features.

We can compute all the principal component and by the definition of eigenvectors, every $P{C}_n$ will be orthogonal to all the other ones before that. As said, the maximum number of PC is the maximum number of dimentions the data is described in.

To perform dimensionality reduction, it’s possible to remove some of the last principal components, since they are the axis that carries the least amount of information. A general idea is to keep the first $k$ principal components, where their cumulative proportion of variance, meaning the variance they express in relationship with the total variance, is 99%.

We then can project the data onto the new $k$-dimensional space, by representing the data with new axis and by maintaining most of the information.

So, in general, PCA is not by itselfe a dimentionality reduction method, but a data transformation method. But since the new space is constructed by principal components that are ordered by the level of variance, it’s possible to delete some of the last one to reduce the number of features

PCA in face recognition

When used in face recognition, principal components gets the name of eigenfaces. Now let’s see in more details how this is used in order to perform face recognition.

We define the traning vector as the vector of dimensions $1\text{ x }n$ that is obtained stretching the images from the trainig set all in one column.

We can form the matrix of training vectors of dimensions $m\text{ x }n$ where $m$ is the number of images in the training set.

We can create the Mean Vector $\bar{x}$ starting from the matrix of training vector by just averaging the value of all the rows. The mean vector will be of dimensions $1\text{ x }n$.

$$\bar{x}=\frac{1}{m}\sum _{i=1}^m{x}_i$$

The mean vector can be represented as an image, and can represent the face that has the most common traits among the all traning set faces.

We can compute the covariance matrix:

$$C=\frac{1}{m}\sum _{i=1}^m(x_i-\bar{x})(x_i-\bar{x}{)}^T$$

The covariance matrix $C$ has dimension $n\text{ x }n$, and so each column can be represented as an image itself.

What we want now is to reduce the dimensionality from $n$ to $k$, where $k$ is the smallest possible number of dimensions that preseve most of the information.

Once we have $C$, we proceed to get the its eigenvectors, which will be our eigenfaces. In order to find an eigenvector $v$, we have to find the eigenvalues $\lambda$ such that $Cv=\lambda v$. We can see that the equation can be rewritten as $|C-\lambda I|=0$ where $I$ is the identity matrix.

Once we have the eigenvalues ${\lambda }_1,{\lambda }_2...$, we put it in the original equation and find the eigenvectors. Source

In order to obtain a $k$-dimension subspace, we order the $k$ eigenvectors that correspond to the highest $k$ values of the matrix. The projection matrix ${\varphi }_k$ is built using the $k$ eigenvectors as columns, and has dimensions $k\text{ x }n$.

The projection of a vector $x$ onto the new $k$-dimension sub-space is defined as following:

$$\text{Proj}(x)={\varphi }_k^T(x-\bar{x})\text{ where }\text{Proj}:{\Re }^n\to {\Re }^k$$

And represent the new feature vector for the image.

The basic idea of PCA for face recognition is that, instead of comparing faces pixels by pixel, which is a technique that gives unreliable results, we can compare images onto the new $k$-dimensional subspace. We can just compare the projetion coefficients $\text{Proj}(x_i)$ corresponding to each image $i$.

The most similar face will have the $\text{Proj}(x^{\prime })$ and calculate the distance between every other feature vector for the images in the gallery. The face more similar will be the least distant to $\text{Proj}(x^{\prime })$.

PCA problems

The main problem of PCA is that it very sensitive to intra-class variations. Meaning that if there are multiple faces of the same subject in the gallery, maybe in different poses (PIE variations), it will be less precise, meaning it may be not able to recognize the same invidivual under different conditions, and lead to false rejections.

Deep Learning Course Definition

Todo

This has to be merged with the content above

PCA - Principal Component Analysis

As we already know, PCA is a dimensionality reduction technique that aims to represent the data points with the first $k$ principal components, where principal components are ordered by the amount of variance they describe.

In matrix notation we represent the $n$ $d$-dimensional data points with the matrix $\mathbb{X}$, the $d$ $k$-dimensional principal components with the matrix $\mathbb{W}$, and the new $n$ $k$-dimensional points, that are the projection of the original points onto the principal components, with the matrix $\mathbb{Z}$.

$$\stackrel{\mathbb{X}}{\overbrace{\underset{n\times d}{\underbrace{\left(\begin{array}{ccc}-& {\mathbf{x}}_1^{\top }& -\\ & ⋮& \\ -& {\mathbf{x}}_n^{\top }& -\end{array}\right)}}}}\stackrel{\mathbb{W}}{\overbrace{\underset{d\times k}{\underbrace{\left(\begin{array}{ccc}|& & \mid \\ {\mathbf{w}}_1& \cdots & {\mathbf{w}}_k\\ |& & \mid \end{array}\right)}}}}=\stackrel{\mathbb{Z}}{\overbrace{\underset{n\times k}{\underbrace{\left(\begin{array}{ccc}-& {\mathbf{z}}_1^{\top }& -\\ & ⋮& \\ -& {\mathbf{z}}_n^{\top }& -\end{array}\right)}}}}$$

Assuming ${\mathbb{W}}^T\mathbb{W}=\mathbb{I}$, for $k<d$ we have:

• Projection: we generate the $\mathbb{Z}$ matrix by projecting the data points onto the principal components.

$$\underset{\text{projection}}{\underbrace{{\mathbb{X}}^T\mathbb{W}}}={\mathbb{Z}}^T$$

• Reconstruction: starting from the reduced representations $\mathbb{Z}$, we want to obtain the original data points $\mathbb{X}$. Of course we won’t exactly get the same $\mathbb{X}$ since we have lost some information.

  $$\mathbb{X}\approx \underset{\text{reconstruction}}{\underbrace{\mathbb{WZ}}}$$

PCA finds the principal components (rows of $\mathbb{W}$) by maximising the sum of orthogonal projections of the data points, that is the same as maximising the variance.

Note

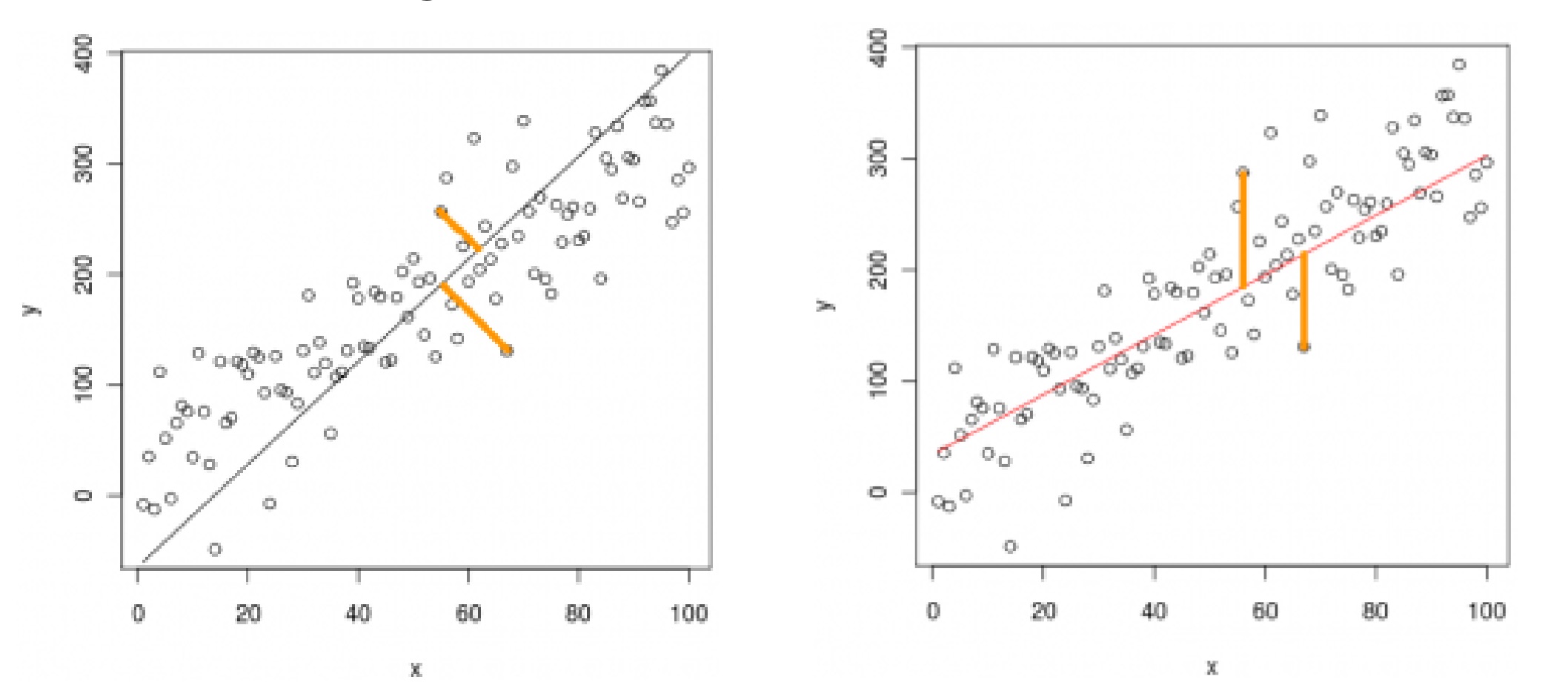
Note that this is fundamentally different from how logistic regression finds the line of best fit, and that the two like won’t be the same most of the time.

With linear regression we measure the error along the $y$ coordinate, with PCA we measure the error orthogonal to the principal direction.

PCA as a generative model

We can use PCA as a generative model by sampling a $z_{\text{new}}\in {\mathbb{R}}^{\mathbb{k}}$ (for example we can take the average of two $z_1,z_2\in {\mathbb{R}}^k$) and using reconstruction in order to obtain the $x_{\text{new}}$ associated.

PCA alone is completely linear, since both the projection and reconstruction operations are linear, so in order to generalize this idea and generate more accurate or complex representations, we will replace the projection and reconstruction operations with two (highly non-linear) neural networks.