Curse of dimesionality

The curse of dimensionality is a phenomena where many points that represent close elements are sparse in the high dimension space and though very difficult to evaluate in a meaningful way.

Sparsity is the factor that causes problem. In statistics, higher the dimension, more data is needed in order to have a significant result from the calculations. More dimensions there are, more sparse will be the points in the dimensions.

In machine learning, the curse of dimensionality is connected to the Hughes effect. The model has to learn a possibly infinite distribution from a finite number of data samples, and more the dimensions, more the data is needed in order to have several examples of each combinations. The need grows exponentially, so the predictive power reduces as the dimensionality increases.

The common theme of these problems is that when the dimensionality increases, the volume of the space increases so fast that the available data become sparse. In order to obtain a reliable result, the amount of data needed often grows exponentially with the dimensionality. Also, organizing and searching data often relies on detecting areas where objects form groups with similar properties; in high dimensional data, however, all objects appear to be sparse and dissimilar in many ways, which prevents common data organization strategies from being efficient.

Alternative Definition (from Deep Learning Course)

Curse of Dimensionality

An image can be represented as a grid of pixels, as an histogram of pixel’s frequency etc. It can also be seen as a point in a $d$-dimensional space, where $d$ is the total number of pixels of the image.

In this space, there are all the possible images with that numbers of pixels. In case of a $1$ megapixel image, the number of pixels (and so dimensions) is $1$ million.

In this highly dimensional space, the number of images to cover all the space is $2^{\mathrm{1.000.000}}$ that is a huge number.

This is the curse of dimensionality, which is a phenomenon where as the dimensions increases, the number of datapoints to cover the space increases in a quadratic way. This makes the space sparse, meaning that the probability of two random points being close to each other is very very low. This is a problem since it makes machine learning models struggle to fit the data.

To overcome this, it’s possible to represent the data with less dimension, using dimensionality reductions methods as PCA; or add more data. The first one being better than the second.

Another important concept is orthogonality. This happens when the inner product between two vector is $0$. In a sparse space, it’s much more probable that two random points are orthogonal between each other than not, since if they’re not it means that they’re very close to each other.

Optimal dimensionality

Even just discovering the intrinsic dimensionality is a challenge.

Note

Manifold learning is a field of machine learning that aims to solve this problem.

This problem is so difficult that today the procedure usually is to fix one dimensionality and try to find the rest of the unknowns. If everything works well than it’s ok, otherwise we try again with another dimensionality.

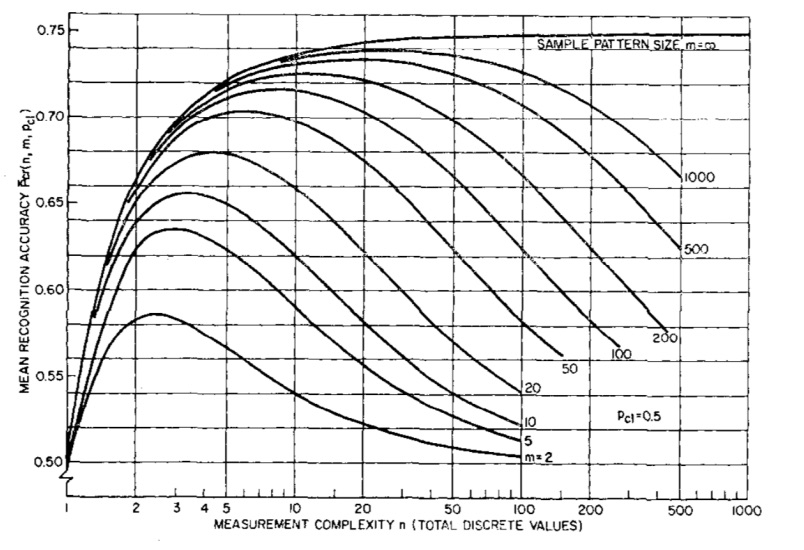
This phenomenon describes how increasing the dimensionality of the data, the model performs better, until a certain peaking point. (Each line is a different model, that can be seen as a different $\sigma$).

Note

The double ascent phenomenon, seen for the first time just a couple of years ago, states that there will eventually exists another peak if the dimensions continue to increase, but this is very computationally expensive.