Regularization

Regularization is a mechanism that reduces overfitting, and so improves generalization.

Any modification that is intended to reduce the generalization error but not the training error can be considered as regularization.

Weight Penalties

$$\underset{\text{loss}}{\underbrace{\ell (\Theta )}}+\lambda \underset{\text{regularizer}}{\underbrace{\rho (\Theta )}}$$

The idea behind weight penalties is to add a regularizer, that is a function weighted by the factor $\lambda$, that increases the loss when the parameters don’t have certain properties.

$\lambda$ controls the trade-off between data fidelitity (that is the part of the loss that directly involves the data) and the model complexity.

Tikhonov (or Ridge) regularization ($L_2$)

In this case:

$$\rho (\Theta )=\Vert \Theta {\Vert }_2=\sum {\theta }^2$$

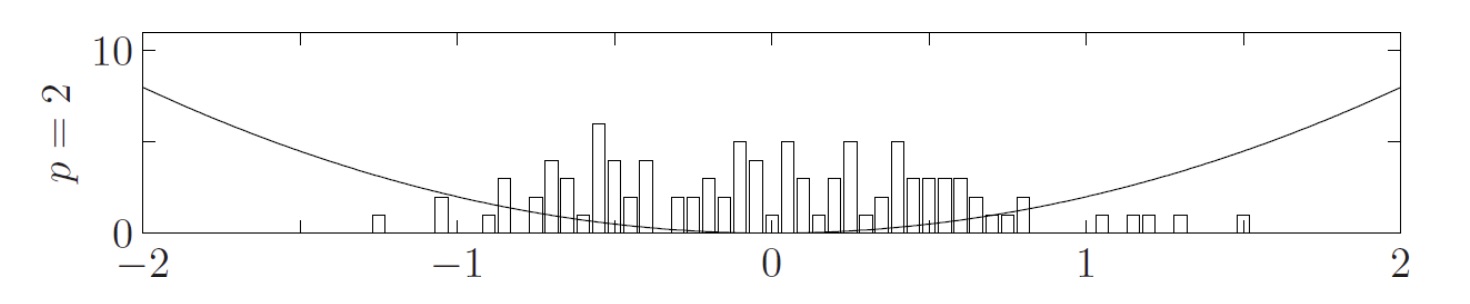
Each bin represent the amount of parameters having that particular value

This type of regularization promotes values for $\theta$ that are in the $[-1,1]$ interval, and so promotes the shrinkage of the parameters $\Theta$.

This because all the $\theta$ that are not in that interval, when squared will result in a quadratically larger value, and so the loss will be incremented.

On the other hand, for values between $-1$ and $1$, the value squared will be smaller, and so the loss will be decremented, and the values promoted.

Lasso regularization ($L_1$)

In this case:

$$\rho (\Theta )=\Vert \Theta {\Vert }_1=\sum |\theta |$$

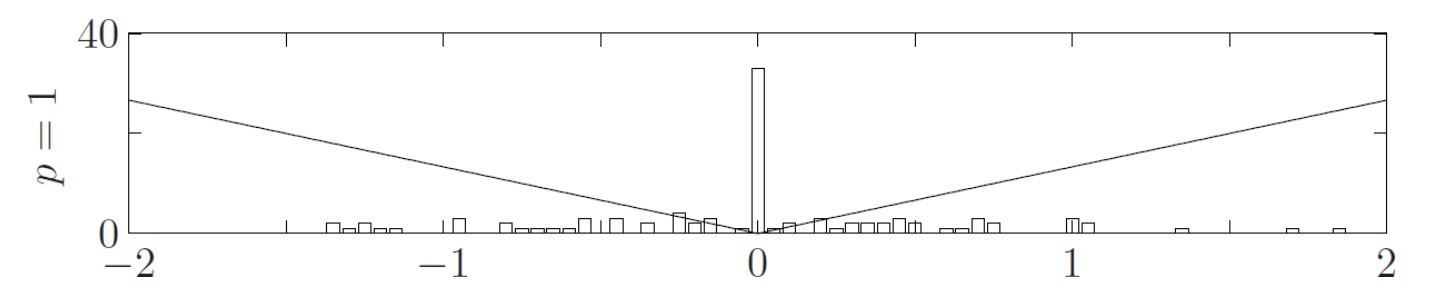
This type of regularization promotes sparsity, meaning that most of the parameters will be equal to $0$.

This because differently from $L_2$ regularization, all the values will be discouraged in proportion with their value, so both numbers far from zero and near zero.

---

We can also use both $L_1$ and $L_2$ regularization, weighting one more than the other using $\alpha$ and $(1-\alpha )$ factors, in order to control the amount of sparsity in $\Theta$. This goes by the name of Elastic net regularization.

In general, we can also bound a type of regularization only to some specific layers.