Geometric Deep Learning

Image can seen as functions defined on ${\mathbb{R}}^2$, and so they represent flat data, since they live on an Euclidean surface. Same thing for audio signals which live on ${\mathbb{R}}^1$.

Geometric deep learning applies deep learning techniques on data that lives on non-Eucildean surfaces, meaning curved surfaces. An example of that are graphs (see Graph Neural Networks) and 3D shapes.

3D shapes in particular can be embedded inside of an Euclidean space, but the shape itself is a manifold.

Non-euclidean data is made of two parts:

• Data: that is the actual data that lives on the surface
• Structure: that are the properties of the surface where the data lives.

Structure is not informative for Euclidean domains, since it’s always the same (images live all on the same surface), but can be very informative for geometric data. The structure of a graph can represent the semantic of the connectivities between nodes, which can be for example the “friend” relationship between nodes, in case of a social network graph. Structure is so informative that we can do learning also only on that.

Rarely we an have a geometric surface with only structure and without data, in this case we can extract the data from the structure itself. For example in case of a manifold, the data at a certain point can be the curvature of the manifold in that point.

The structure of the geometric surface can also change over time, and this should or shouldn’t affect our deep learning algorithm. For example we may want a pose classifier for 3D shapes of people, and in this case it should be pose-variant. In case of a people recognizer from 3D shapes, we want the model to be pose-invariant, since we want to recognize a person regarding of its pose. This is something that is never considered for regular flat data.

Convolution on Geometric data

We can try to apply convolution on 3D shapes with 3D kernels, just like it happens for euclidean surfaces. This works well until the structure of the shape changes, in this case the result will be completely different. This is called extrinsic convolution.

In order to solve this problem, we can perform an intrinsic convolution, in which the convolutional kernel lives on the shape surface (and not in the embedding space), in order for it to change together with the structure. In this case the convolution will be invariant to that change.

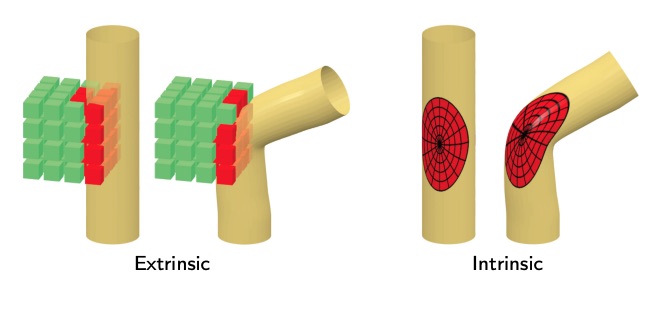
This is a major difference, since If I want to train a classifier with extrinsic convolution, I need to train it with all the possible poses, hence it’s undoable.

Note

To perform convolution we need also the data, and not only the structure.

In order to have a convolution operator (i.e. any operator that is shift invariant) we have to come up with the notion of shift, that’s not so simple as for euclidean domains. This is not trivial both for surfaces and graphs. (What nodes should be inside the convolution with a certain node. For example every node at distance $k$, of the nodes that have some degree $\alpha$). An approach for graph convolutons can be seen in the linked page.

Local ambiguity

If I have two graphs (represented with an adjacency matrix), that are the same graph but permuted, meaning the matrix has a different ordering, I have to be invariant to the permutation. This also doesn’t happen with images, since we are going to apply always the same canonical order (top left first pixel, or something else). Graph isomorphism is an NP-hard problem.