Invariances and Equivariances

Translation Invariance

Being invariant with respect to an operator means that the result of the operation doesn’t change if that operator is applied.

If we build a classificator $\mathcal{C}$ that tells us if the image contains a cat or not, the result should be the same if the cat is translated inside the image.

We define the (linear) translation operator $\mathcal{T}$ along a vector $v\in {\mathbb{R}}^2$ as:

$${\mathcal{T}}_{v}f(x)=f(x-v)$$

Where $v$ lives in the same domain of the function $f$, that is, in this case, the function that represent the image. $v$ is just the displacement vector, that translate each pixel to another point in the space.

For $\mathcal{C}$ to be translation-invariant, means that:

$$\mathcal{C}({\mathcal{T}}_{v}f)=\mathcal{C}(f)\forall f,{\mathcal{T}}_v$$

Both the domain and codomain of $\mathcal{T}$ is a function space, because it takes in input a function (the image) and returns another function (the translated image).

We can prove that the operator is linear, since it is homogeneous and additive.

Note

The operator will be still linear with respect to $f$ even if inside $f$ we would have some non-linear complex function instead of $x-v$.

Shift-equivariance

Furthermore, convolution is translation-equivariant (or shift-equivariant), meaning that the result doesn’t change if we first apply translation, and then convolution or vice-versa:

$$f\left(x-x_0\right)\star g(x)=(f\star g)\left(x-x_0\right)$$

Note

Watch out that invariance and equivariance are two very different things! Being invariant from an operator means that the result doesn’t change; being equivariant means that we can invert the order of the operations and the result won’t change.

Shift-equivariance: if I invert the order of the translation-convolution operation the result remains the same

This type of equivariance allow us to define in another way convolutions:

Any linear operator that is shift-equivariant is a convolution

Extra: other types of invariances

Other types of invariances are possible, for example invariance to partiality and isometric deformations. This is useful if we have a 3D morphable model of a dog, and we want to be invariant if the model is morphed in another position. This is an hard problem.

---

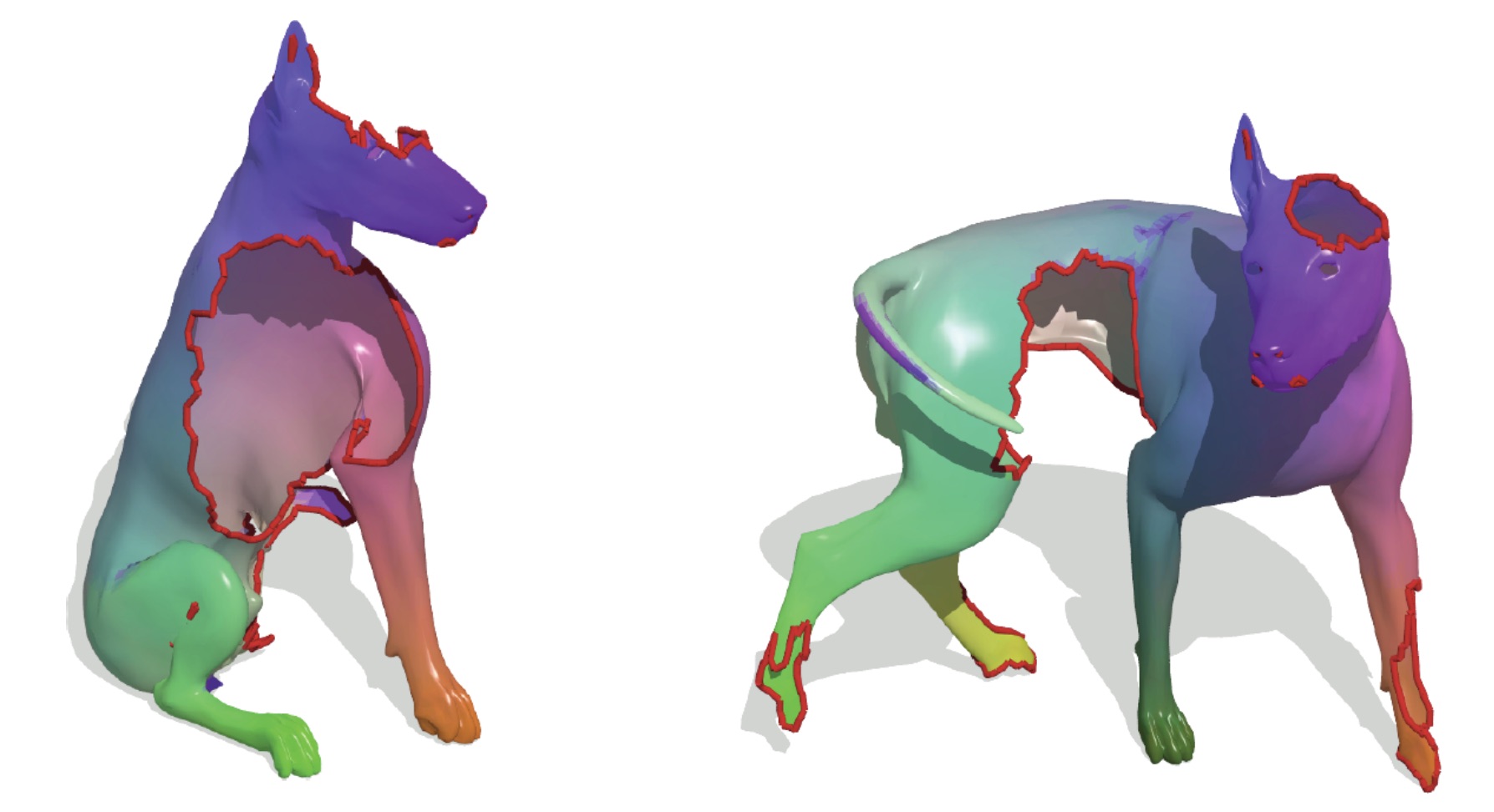
We want translation invariance across multiple scale, and in fact we expect local features to be invariant to their location in the image (since they’re local, and so we don’t care where in the image they are).

This means that:

$$z({\mathcal{T}}_{v}p)=z(p)\forall p,{\mathcal{T}}_v$$

Where $p$ are the patches of variable size (local features).

Note

CNNs only give us translation invariance, and not rotation invariance, since rotation is not translation.