Activation Functions

All activation function are used to introduce some non-linearity in the network, but depending on the network, some function are able to mitigate some other problems and make the learning process more stable.

Sigmoid

Sigmoid is the first activation function ever used. It was created to simulate the firing rate of a brain neuron.

$$\sigma (x)=\frac{1}{1+e^{-x}}$$

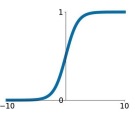
The function squashes the input $x$ into a range of $[0,1]$.

The sigmoid has $3$ problems:

1. If we analyze the function, we can see that the function can kill the gradients if the input $x$ is not close to $0$ (positively or negatively). Because the gradient of the function w.r.t to $x$ si defined as:

   $$\frac{\partial \sigma (x)}{\partial x}=\sigma (x)(1-\sigma (x))$$

   This will produce the problem of vanishing gradients.

2. Another problem is the fact that the elements in the gradient vector have all the same sign, which is bad because we only can update the weights with all positive or all negative deltas. In practice this means that we can only “zig-zag” into the optimal path, which will result in a slower convergence. This isn’t really a big problem because of mini batches, and because this happens only for each sample, so we update with different signs for each sample.

3. The third problem is the fact that the exponential is a bit expensive in terms of computation complexity.

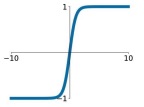
Tanh

Tanh is similar to the sigmoid and it resolves the two problems apart from vanishing gradients.

ReLU (and its variants)

Introduced with AlexNet, the Rectifier Linear Unit function solves a lot of problems.

$$\text{ReLU}(x)=\max (0,x)$$

First of all it doesn’t kill the gradients for positive $x$s. It’s also very efficient and allows a faster convergence.

The two problems are that gradients are killed for negative $x$s, and the fact that is not zero-centered like sigmoid or tanh. Here we will introduce some ReLU variants that aim to solve some of these problems:

• $\text{Leaky ReLU}(x)=\max (0.1x,x)$: doesn’t kill the gradients by introducing a small coeficient.
• $\text{Parametric ReLU}(x)=\max (\alpha x,x)$: like the Leaky ReLU, but makes the coefficeint $\alpha$ learnable.
• $\text{ELU}(x)=\{\begin{array}{llc}x& & x\ge 0\\ \alpha (e^x-1)& & x<0\end{array}$: Exponential Linear Unit, which is less efficient because of the exponential computation.
• $\text{SELU}(x)$: Scaled ELU, which is better for deep networks since it has a self-normalizing properties and so it doesn’t need Batch Norm.

Maxout

Maxout generalizes the ReLu and the Leaky ReLU by inserting two learnable linear layers, one in each side. Both the functions are linear, and there is no exponential. It doesn’t saturate nor die. The only problem is that it doubles the number of parameters (one network per side of the maxout).

$$\max (w_1^{T}x+b_1,w_2^{T}x+b_2)$$

Note

The rule of thumb is to use ReLU and see how it goes, then try to use one of its variants (including Maxout) to squeeze out some marginal gains. Don’t use sigmoid or tanh!