Autoencoders

When we generalize the idea behind the PCA as generative model, we call the projection and reconstruction procedures respectively encoding and decoding.

The encoder will be a function (neural net) that takes a data point $x$ in input and outputs a low-dimensional code $z\in R^k$ that is the intermediate representation of $x$.

The decoder will take the code $z$ and return the $x$ that is the most similar to the one that generated $z$.

An architecture like this, in which encoder and decoder put together generate an output $x$ that is the most similar to the input. (If this doesn’t happen, then it’s just an encoder-decoder architecture).

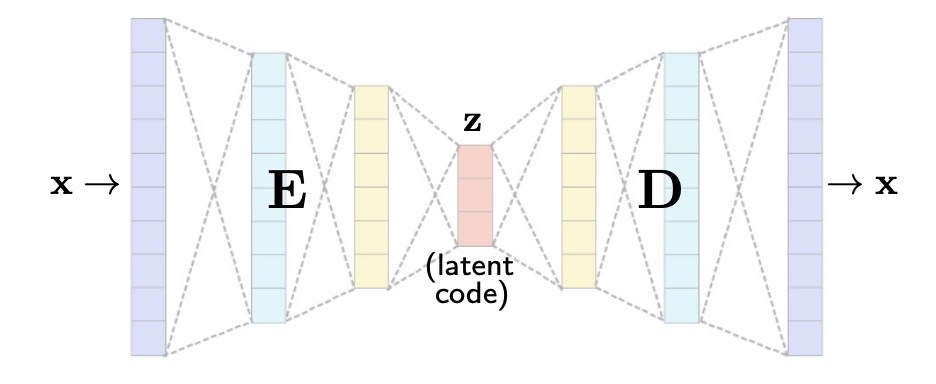
In order to enforce the Autoencoder to learn the encoder and decoder such that it will output a vector that is very similar to the input, we have to enforce it into the loss function:

$$\underset{\text{reconstruction loss}}{\underbrace{{\ell }_{\theta }=\sum _i\Vert x_i-D_{\Theta }(E_{\Theta }(x_i))\Vert }}$$

The type of norm depends on the data, if we have data that lives in the euclidean space, than we can use the $L_2$ norm.

💡 If the layers of the NN are linear, than the codes $\mathbb{z}_i$ span the same space as PCA.

Importance of the bottleneck

The bottleneck in the architecture, meaning the fact that $k<d$ is important in order to avoid trivial solutions.

• If $k=d$, then $z\in {\mathbb{R}}^d$ and so we risk that both the encoder and decoder will learn the identity function (meaning that $z=x$)
• If $k>d$, then we risk that the encoder and decoder will just create the $z$ as $x$ concatenated with as much $0$ needed in order to arrive to the $k$ dimensions.

Variational Autoencoders (VAE)

When dealing with simple autoencoders, we can have some regions of the space space in which the codes are immersed that have blanks, and so when we sample out of that blank and then decode the result, we won’t obtain an image that is natural. This because there aren’t enough points near that point.

The idea to resolve this problem is to enforce the latent space to be packed within a smaller area, and so to be dense, in order to avoid blanks.

Variational autoencoders are a type of autoencoders that allow to do that, in particular they allow to enforce a distribution in the latent space, meaning that it will produce codes that can be seen as samples from that probability distribution. In other words, if we sample the code from the latent space, then the sampling should respect the probability distribution that we enforced.

The distribution is chosen a priori, and most of the time it’ll be a Gaussian.

💡 There is no proof that we are loosing information by going from autoencoders to variational autoencoders. We are just placing the embeddings in a different way.

## Variational inference

In our scenario $x$ is a given data point and $z$ is a latent code.

In a variational autoencoder architecture, the encoder take in input a data point and returns the probability distribution of all possible latent codes.

$$p_{\theta }(z|x)=\frac{p_{\theta }(x|z)p_{\theta }(z)}{p_{\theta }(x)}=\frac{p_{\mathbf{\theta }}(\mathbf{x},\mathbf{z})}{p_{\theta }(x)}$$

The problem here is that we cannot exactly compute that, because we cannot compute:

$$p_{\theta }(x)=\int p_{\theta }(x|z)p_{\theta }(z)dz$$

Since we need to integrate over the entire latent space, which we don’t have. So the problem is intractable.

What we can do is to compute an approximation:

$$q_{\mathbf{\varphi }}(z|x)\approx p_{\theta }(z|x)$$

where $q_{\varphi }(z|x)$ is a neural net with weights $\mathbf{\varphi }$. In order to let the neural net learn the best parameters ${\mathbf{\varphi }}^{\ast }$ we have to enforce the fact that we want the two distributions to be as close as possible in the loss function, by minimizing the $KL$ divergence.

$$\begin{array}{r}{\mathbf{\varphi }}^{\ast }={\text{argmin}}_{\mathbf{\varphi },\mathbf{\theta }}KL(q_{\mathbf{\varphi }}(z|x)||p_{\theta }(z|x))\\ \text{after some calculations}\\ =\arg \underset{\mathbf{\varphi },\mathbf{\theta }}{\max }\sum _{\mathbf{z}}{q}_{\mathbf{\varphi }}(\mathbf{z}\mid \mathbf{x})\log \frac{p_{\mathbf{\theta }}(\mathbf{x},\mathbf{z})}{q_{\mathbf{\varphi }}(\mathbf{z}\mid \mathbf{x})}-\log p_{\mathbf{\theta }}(\mathbf{x})\end{array}$$

The $-\log p_{\mathbf{\theta }}(\mathbf{x})$ contains the intractable term and so there still is a problem, but this is solvable noticing that, applying at theorem, the right part of the equation is always bigger than the left part, and so the maximisation of only the left part will approximate the maximisation of the whole thing.

The right part takes the name of Evidence variational Lower BOund or $ELB{O}_{\varphi ,\theta }(x)$.

We are interested in finding:

$$\begin{array}{r}\underset{\mathbf{\varphi },\mathbf{\theta }}{\max }ELB{O}_{\mathbf{\varphi },\mathbf{\theta }}\\ =\underset{\mathbf{\varphi },\mathbf{\theta }}{\max }\sum _{\mathbf{z}}{q}_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})\log \frac{p_{\mathbf{\theta }}(\mathbf{x},\mathbf{z})}{q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})}\\ =\underset{\mathbf{\varphi },\mathbf{\theta }}{\max }\sum _{\mathbf{z}}{q}_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})\log p_{\mathbf{\theta }}(\mathbf{x}|\mathbf{z})+\sum _{\mathbf{z}}{q}_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})\log \frac{p_{\mathbf{\theta }}(\mathbf{z})}{q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})}\\ =\underset{\mathbf{\varphi },\mathbf{\theta }}{\max }\underset{\text{likelihood of observing }x\text{ given }z}{\underbrace{{\mathbb{E}}_{q_{\mathbf{\varphi }}(\mathbf{z}\mid \mathbf{x})}\log p_{\mathbf{\theta }}(\mathbf{x}|\mathbf{z})}}\underset{\text{ensures }{q}_{\varphi }(z|x)\approx p_{\theta }(z)}{\underbrace{-KL\left(q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})\Vert p_{\mathbf{\theta }}(\mathbf{z})\right)}}\end{array}$$

The first part of this equation is simply the reconstruction loss, and we can also substitute it with the loss ${\ell }_{{}_{\varphi },\theta }$ we’ve seen before.

The second term is the $KL$ divergenge, and it’s needed in order to enforce the encoder $q_{\varphi }$ to be the most similar to the true function $p_{\theta }$, this is the regularizer.

Since we want to maximise that, it’s the same as minimizing the negative, so the loss is just:

$${\ell }_{\varphi ,\theta }=-\underset{\text{reconstruction loss}}{\underbrace{{\mathbb{E}}_{q_{\mathbf{\varphi }}(\mathbf{z}\mid \mathbf{x})}\log p_{\mathbf{\theta }}(\mathbf{x}|\mathbf{z})}}+\underset{\text{regularizer}}{\underbrace{KL\left(q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})\Vert p_{\mathbf{\theta }}(\mathbf{z})\right)}}$$

Remember that the probability distribution is chosen a priori, so for example we choose $p(z)={\mathcal{N}}_{0,\mathbb{I}}(z)$, and so we can forget about the parameters $\theta$, because the probability distribution has no free parameters.

The probabilistic encoder $q_{\varphi }(z|x)$ also generates a Gaussian distribution (if we choose the Normal distribution) with some mean $\mathbf{\mu }$ and a standard variation $\mathbf{\sigma }$, different for each data point $x$ (of course the output changes also according to the neural net parameters $\varphi$).

The difference of a probabilistic encoder from a simple encoder is that it outputs the mean and the standard variation, from which we can sample each time a different $z$, instead of outputting directly the $z$.

The Gaussian is most of the time the best choice, also because using that the $KL$ term has a closed form.

💡 To distinguish VAE from AE, the latter are also called deterministic AE.

Regularizing effect

Reparametrization trick