Jensen’s inequality

Jensen’s inequality states:

$$f(\alpha x+(1-\alpha )y)\le \alpha f(x)+(1-\alpha )f(y)$$

Meaning that taking two points $(x,f(x))$ and $(y,f(y))$ of a convex function, every point on their linear convex combinations (meaning the set of all points on the line that crosses the two points) is bigger than the point at that coordinate taken on the actual curve.

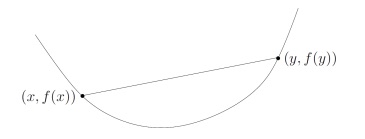
Visual representation of Jensen’s inequality

If Jensen’s inequality is true for each possible pairs of points of a function, than the function is convex.

We can find the minimum by computing the derivative of the function and putting it to zero. If the function is convex, than we have the guarantee that there is only a minimum; if the function is non-convex, than there may be multiple minima, and only one global minimum.

In a convex function, the global minimizer $x$ is where $\frac{df(x)}{dx}=0$.

The Jensen’s inequality principle is true also for more than two dimensions. In this case the notion of derivative is replaced with the notion of gradient, that is the vector of partial derivative with respect to each single parameter.

$${\nabla }_{x}f(x)=\left(\begin{array}{c}\frac{\partial f}{\partial x_1}\\ ⋮\\ \frac{\partial f}{\partial x_n}\end{array}\right)$$

We also have the global optimality condition, that states:

$${\nabla }_{x}f(x)=0\to f(x)\le f(y)\forall y\in {\mathbb{R}}^n$$